Coefficient de corrélation de concordance
Le coefficient de corrélation de concordance est un des tests statistiques permettant de mesurer l’accord entre deux méthodes, deux observateurs etc. Contrairement au coefficient de corrélation intraclasse (ICC), il ne présuppose pas que les prérequis de l’ANOVA soient remplis. Il peut être utilisé dès 10 paires d’observations.
Il n’y a pas de règles publiées dans des journaux revus par les pairs quand à l’interprétation du CCC. Il convient d’adapter l’interprétation au niveau d’exigence requis.
Les codes R ci dessous présentent quelques situations de comparaison entre deux variables, afin de voir à l’aide d’exemples comment le CCC se comporte.
####comparaison de deux variables proches####
#Deux variables équivalentes se distribuent autour de la droite d'équation y=x (en rouge)
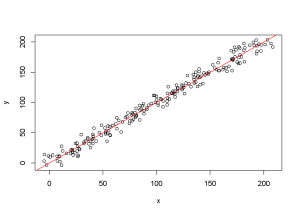 # le CCC est proche de 1 quand les variables sont très similaires :
CCC
est lower upper
0.9901 0.987 0.9925
#Trois éléments peuvent être examinés pour mieux comprendre la source des variations du CCC:
#Le scale shift de variables équivalentes est proche de 1. Il mesure la différence de pente entre la droite de régression des variables et la droite d'égalité d'équation y=x (en rouge).
Scale shift
1.006
#le location shift de variables équivalentes est proche de 0. Il mesure la distance de la droite de régression des variableset la droite d'égalité d'équation y=x (en rouge).
Location shift
0.005347
#Le dernier élément est un facteur de correction du biais, qui mesure la déviation de la droite de régression des variables par rapport à la droite d'équation y=x, Il est proche de 1 quand il n'y a pas de déviation (variables équivalentes).
epi.ccc(x,y)$C.b
1
#la pente de la droite de régression entre les deux variables est différente de la droite d'équation y=x (en rouge)
# le CCC est proche de 1 quand les variables sont très similaires :
CCC
est lower upper
0.9901 0.987 0.9925
#Trois éléments peuvent être examinés pour mieux comprendre la source des variations du CCC:
#Le scale shift de variables équivalentes est proche de 1. Il mesure la différence de pente entre la droite de régression des variables et la droite d'égalité d'équation y=x (en rouge).
Scale shift
1.006
#le location shift de variables équivalentes est proche de 0. Il mesure la distance de la droite de régression des variableset la droite d'égalité d'équation y=x (en rouge).
Location shift
0.005347
#Le dernier élément est un facteur de correction du biais, qui mesure la déviation de la droite de régression des variables par rapport à la droite d'équation y=x, Il est proche de 1 quand il n'y a pas de déviation (variables équivalentes).
epi.ccc(x,y)$C.b
1
#la pente de la droite de régression entre les deux variables est différente de la droite d'équation y=x (en rouge)
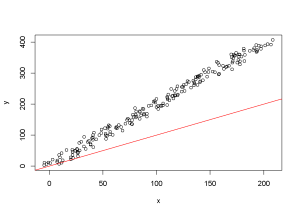 # les variables sont différentes, et le CCC est différent de 1 :
CCC
est lower upper
0.4982 0.4485 0.5448
Scale shift
1.972
Location shift
1.23
epi.ccc(x,y)$C.b
0.5012
####comparaison de deux variables d'ordonnée à l'origine différente####
#Deux variables équivalentes se distribuent autour de la droite d'équation y=x (en rouge)
# les variables sont différentes, et le CCC est différent de 1 :
CCC
est lower upper
0.4982 0.4485 0.5448
Scale shift
1.972
Location shift
1.23
epi.ccc(x,y)$C.b
0.5012
####comparaison de deux variables d'ordonnée à l'origine différente####
#Deux variables équivalentes se distribuent autour de la droite d'équation y=x (en rouge)
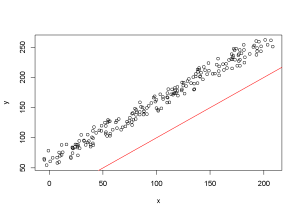 CCC
est lower upper
0.6515 0.6032 0.6951
Scale shift
0.9955
Location shift
1.017
epi.ccc(x,y)$C.b
0.6589
####comparaison de deux variables de pente et d'ordonnée à l'origine différentes####
#Deux variables équivalentes se distribuent autour de la droite d'équation y=x (en rouge)
CCC
est lower upper
0.6515 0.6032 0.6951
Scale shift
0.9955
Location shift
1.017
epi.ccc(x,y)$C.b
0.6589
####comparaison de deux variables de pente et d'ordonnée à l'origine différentes####
#Deux variables équivalentes se distribuent autour de la droite d'équation y=x (en rouge)
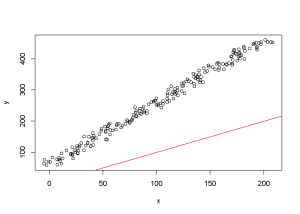 CCC
est lower upper
0.3162 0.2731 0.3581
Scale shift
2.004
Location shift
1.945
epi.ccc(x,y)$C.b
0.3181
####comparaison de deux variables de variance différente####
#Deux variables équivalentes se distribuent autour de la droite d'équation y=x (en rouge)
CCC
est lower upper
0.3162 0.2731 0.3581
Scale shift
2.004
Location shift
1.945
epi.ccc(x,y)$C.b
0.3181
####comparaison de deux variables de variance différente####
#Deux variables équivalentes se distribuent autour de la droite d'équation y=x (en rouge)
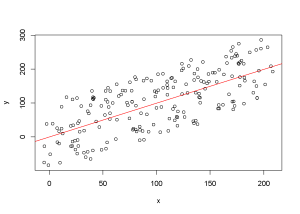 # le CCC est proche de 1 quand les variables sont très similaires :
CCC
est lower upper
0.6697 0.5962 0.732
Scale shift
1.438
Location shift
0.05126
epi.ccc(x,y)$C.b
0.9363
# le CCC est proche de 1 quand les variables sont très similaires :
CCC
est lower upper
0.6697 0.5962 0.732
Scale shift
1.438
Location shift
0.05126
epi.ccc(x,y)$C.b
0.9363
